状態マシン図(State Machine Diagram)
状態マシン図とは、オブジェクトの状態遷移を表現する為の図です。各状態の内容および、状態遷移の条件等を記述します。
記述例
下の図は、中学校を卒業した状態から大学生の状態になるまでを表した例です。
【要件定義】
「大学生」になるためには、高校を卒業、もしくは大学入学資格の取得を経て、大学受験で合格する必要があります。
高校を卒業するためには、「一年生」、「二年生」、「三年生」と各学年に進級する必要があり、高校に進学せず大学入学資格を取得するには、大学入学資格検定に合格する必要があります。

遷移を表す矢印に、記述されている「受験[合格]/入学」は、「契機[条件]/効果」の書式で記述されています。つまり、大学生になるには、受験で合格して大学に入学するという意味になります。
このように、状態マシン図を記述することによって、実体の状態変化を、順を追って詳細に記述する事が出来ます。
構成要素
状態マシン図は次の要素で構成されます。
| 要素 | 表示形式 | 意味 |
| 開始状態(begin state) |
|
スコープ内で開始を表します。 |
| 終了状態(sink state) |
|
スコープ内で終了を表します。 |
| 状態(1)(state) |

|
実体の状態を表します。 |
| 状態(2)(state) |

|
実体の状態に対して、機能も明記して表します。 |
| 遷移(transaction) |
|
一つの状態から別の状態への遷移を示す矢印です。契機、条件、効果はそれぞれ省略可能です。 |
| 平行(concurrent) |
|
複数の平行状態の発生・収束を意味します。 |
| 選択仮状態(conditional pseudo state) |
|
前の状態を受けて、次の状態を選択するための仮状態を表します。 前の状態が、遷移条件を示すガードに合致する方へ状態遷移します。複数の条件に合致した場合は、その遷移先は任意となり、合致するものが無い場合は記述の誤りとみなします。 |
| 交差状態(junction) |
|
二つ以上の遷移が集約される状態、または、二つ以上の遷移が離散する状態、もしくはその両方が起こる状態を表します。 |
| 合成状態(1)(composite state) |

|
下位に二つ以上の状態を包括する状態を表します。 |
| 合成状態(2)(composite state) |

|
合成状態(1)の略式表記です。 |
| エントリー状態(entry state) |
|
合成状態の入り口を表します。 |
| イグジット状態(exit state) |
|
合成状態の出口を表します。 |
| 停止状態(terminate node) |
|
終了状態は、一つの処理などで、開始状態に対する終了を表しますが、停止状態は、状態マシン図で定義されている事象そのものが完了することを表します。 |
| 領域(region) |

|
ある状態は、個々に独立した状態を総合したものであることを表します。 |
| 状態リスト(state list) |

|
複数の状態を、ある共通項で結んだ表現となります。状態を反復処理させる場合などによく用いられる表現です。 |
| 浅い履歴状態(history, shallow pseudo state) |
|
以前状態にもどることを表します。浅い履歴状態では、形式的に戻ることを意味しており、実際に遷移前と遷移後とで以前の状態に変化があっても、考慮しません。 |
| 深い履歴状態(history, deep pseudo state) |
|
以前状態にもどることを表します。深い履歴状態では、実際に遷移前と同じ状態に戻します。 |
各要素の記述例
基本構成
下の図は、次のバスを待つ乗客を表した例です。

【解説】
バスを待っている状態は、バスが到着すると乗車できるので終了します。
選択仮状態、交差
下の図は、登山の工程を表した例です。

【解説】
山を登り、頂上に到着すると、記念撮影をするなど休憩して、その後、下山します。もし登っている途中で、けが人が発生した場合は、すぐに下山します。天候が悪化した場合は、天候が回復するまでキャンプをして、その後、再度山登りの状態になります。
合成状態、停止状態
下の図は、携帯電話の充電状態を表した例です。

【解説】
携帯電話の起動中の状態は、「充電が完了している状態」、「電池の残量が十分残っている状態」、「電池の残量が少なくなった状態」から成り立っています。もし「電池の残量が少なくなった状態」で電池が切れた場合は、停止状態となり、状態遷移は完全に終了します。
領域
下の図は、健康診断を表した例です。

【解説】
「診察」という状態は、三つの状態(「体温検査」、「血液検査」、「胃腸検査」)を持った合成状態ですが、この三つの状態は、それぞれ独立しており、お互いに状態遷移することはありません。
このように包括されている各状態が独立している(互いに遷移しない)ような場合、状態を点線で区切って、領域を作成し、状態遷移を整理することが出来ます。
状態リスト
下の図は、トーナメントの組合せ抽選を表した例です。
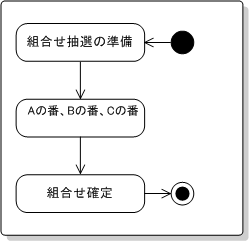
【解説】
抽選はA、B、Cと順番に行いますが、それぞれの状態(「Aが抽選を行っている状態」、「Bが抽選を行っている状態」、「Cが抽選を行っている状態」)を「抽選を行っている状態リスト」として表現しています。
浅い履歴状態
下の図は、野球の試合を表した例です。

【解説】
野球の試合中に雨が降ってきた場合、一時中断します。その後、雨が止まなければ再試合となり、後日に再開されますが、中断時点の状況までは再現されません。
深い履歴状態
下の図は、野球の試合を表した例です。

【解説】
野球の試合中に雨が降ってきた場合、一時中断します。その後、雨が止むと試合は再開されますが、中断時点の状況を忠実に再現して再開されます。